死せる詩人のWeblogです。読書記録とDungeons and Dragons Role Playing Gameのセッション記録が主です。リンクは御自由にどうぞ。
2017年11月28日火曜日
心理統計学の基礎 第四章 備忘録
## Sec1
母集団
標本 (サンプル)
標本抽出 (サンプリング)
単純無作為抽出
二段抽出 : 母集団から部分集団をランダムに選択して、部分集団から更にランダムで標本抽出。
統計的推測の前提
個々のデータ (標本) が互いに独立に同じ確率的振舞いをすること。
この前提を満たす為には単純無作為抽出が必要。
例えば中学生の試験点数の例で言うならば、部分集団として適当な中学校を選んだとしてその学校が進学校で平均的に学力が高い場合、その部分集団としての進学校から標本抽出するとデータに偏りが発生する。
標本統計量
標本から得られる平均値や相関係数などの記述的指標の事。
母集団から得られる値は「母数」と言う。
標本値と母数を区別する場合、標本平均、標本相関係数、母集団平均、母集団相関係数などと呼ぶ。
確率モデル
母集団を一種のデータ発生装置と見做して、標本抽出によって各データがどういう確率でどういう値を取るか、を模式化したもの。
確率変数
確率的に変動する変数。
確率分布
確率変数がどういう確率でどういう値を取るかの分布。
標本分布
標本統計量がどういう確率でどういう値を取るかを表わす分布。特定の標本におけるデータの度数分布ではない。度数分布というのは観測データから得られた具体的な値の集合で、標本分布 (確率分布) というのは理論的に導出された抽象的なもの。
二値変数
一般に yes/no で分類できるような値を 0/1 で表わす変数。
二項分布
成功確率 $p$ の試行を独立に $n$ 回繰り返した時の成功数 $k$ を与える分布。例えば d20 を 100 回 ($n=100$) 振って出目 20 ($p=0.05$) が 5 回出る ($k=5$) 確率などにあたる。以下の式で表わされる。
\[
f (w)={}_{n}C_{k}p^{k}(1-p)^{N-k}
\]
${}_{n}C_{k}$は以下の式で表わされる組み合わせ総数 ($n$ 種類のものから $k$ 個を選択する組み合せの数)。
\[
{}_{n}C_{k} = \frac{n!}{k! (n-k)!}
\]
従って前式は
\[
f (w) = \frac{n!}{k! (n-k)!}p^{k}(1-p)^{N-k}
\]
となる。$N=1$ の場合を特にベルヌーイ分布と言う。
確率分布に於ける確率変数 $x$ の分布の平均 $μ$ は
\[
μ=\sum_{k=1}^{m}x_{k}f (x_{k})
\]
不偏性
標本統計量の分布の平均が、母数の値に一する時その統計量は不偏性を持つ、と言う。不偏性を持った統計量は不偏推定量と呼ばれる。
確率分布の標準偏差
確率分布 $f (x)$ に従う確率変数 $x$ の標準偏差 $σ$ は度数分布の標準偏差と同じように以下の式で与えられる。
\[
σ=\sqrt{\sum_{k=1}^{m}(x_{k}-μ)^{2}f (x_{k})}
\]
上式の $f (x_{k})$ に二項分布の式を代入し式変形すると
\[
σ_{w}=\sqrt{Np (1-p)}
\]
が得られる。この式を N で割る事によって得られる
\[
σ_{p}=\frac{\sqrt{Np (1-p)}}{N}
\]
は比率の標本分布の標準偏差である。
標本統計量は、標準偏差が大きい程その統計量に基づく母数の推定の誤差が大きくなる可能性が高い。標本統計量の標準偏差は、標準誤差とも呼ばれる。標本数 N が大きくなる程、標準誤差は小さくなる。
逆に標準誤差を特定の値以下に抑えるのに必要な標本数を計算によって求める事が出きる。標準誤差の式を用いて、例えば比率 $p$ の標準誤差を 5%以下にしたいのであれば
\[
σ_{p}=\frac{\sqrt{Np (1-p)}}{N}\leq0.05
\]
という不等式を立ててこれ解く。
\[
N\geq400p (1-p)
\]
右辺は $p=0.5$の時に最大になるので
\[
N=400\times0.5\times0.5=100
\]
となって標本数を 100 以上にすれば比率 $p$ の標準誤差を 5%以下に抑えられる。
## Sec3
正規分布
確率密度関数
確率変数が、二項分布の様な離散値では無く連続値を取る場合の確率分布は、その変数が特定の値を取る確率では無く、ある範囲の値を取る確率を問題する。そのような確率は分布の確率密度関数を用いて計算される。
平均 $μ$、標準偏差 $σ$ の正規分布に従う変数 $x$ の確率密度関数は
\[
f (x)=\frac{1}{\sqrt{2p σ}}\exp [-\frac{(x-μ)^2}{2 σ^{2}}]
\]
と表わされる。この変数がある特定の範囲 (a<x<b) の値を取る確率 $Prob (a<x<b)$ は
\[
Prob (a<x<b)=\int_{a}^{b}f (x) dx
\]
によって与えられる。
標準正規分布
平均 0、標準偏差 1 の正規分布。
中心極限定理
標本数を大きくしていくと、母集団の分布の種類とは無関係に標本平均の分布が正規分布に近付いていくという定理。
## Sec4
二変数正規分布
連続値を持つ 2 つの独立した確率変数を要素としてもつ正規分布。一変数正規分布は平面で表わされるが、二変数の場合立体図になる。
二つの変数を $x$、$y$ とした時、それぞれの平均を $μ_{x}$、$μ_{y}$、標準偏差を $σ_{x}$、$σ_{y}$、$x$ と $y$ の相関係数を $ρ$ とした時の確率密度関数は
\[
f(x,y)=\frac{1}{2pσ_{x}σ_{y}\sqrt{1-ρ^{2}}} \times exp[-\frac{z_{x}^{2}-2ρz_{x}z_{y}+z_{y}^{2}}{2(1-ρ^{2})}]
\]
ただし $z_{x}$、$z_{y}$ は
\[
z_{x}=\frac{x-μ_{x}}{σ_{x}}\\
z_{y}=\frac{y-μ_{y}}{σ_{y}}\\
\]
相関係数の標本分布
データが二変数正規分布に従う時の相関係数 $r$ の標本分布は母集団相関係数 $ρ$ と標本数 $N$ のみによって規定される確率分布になる。
## Sec5
頑健性
仮定した確率モデルの分布が、母集団分布と異なる時に、モデルに基づく推定が妥当である程度の事。一般に標本数が大きくなれば母集団分布の違いの影響は小さくなり頑健性が増す。
ノンパラメトリック法
特定の分布形を仮定しない方法
【今日の読書】CIAの秘密戦争 変貌する巨大情報機関
著者: マーク・マゼッティ
監訳: 小谷 賢
訳者: 池田 美紀
出版: 早川ノンフィクション文庫
ISBN: 978-4-15-050504-2
2017年11月26日日曜日
MacBookPro 13 インチ 2012 Mid の SSD 化
僕のメインの計算機は 2012 年に購入した MacBookPro (以後 MBP) の 13 インチ、2012 Mid モデルです。
既に 5 年使っているのですが、最近アプリケーションの起動速度が遅い事が気になってきました。また 1 年程前に、内蔵スロットイン DVD が、DVD を飲み込んで吐き出さなくなってしましました。
調べてみるとハードディスクを SSD に換装すれば速度の問題はかなり改善しそうです。また内蔵の DVD ドライブも簡単に交換出来そうなのでやってみる事にしました。
必要物品
まず準備。交換部品は以下の通りです。
SSD: Crucial 2.5 インチ MX300 275GB DVD: CrownTrade Macbook 対応用 パナソニック UJ-898 交換用 DVD ± R/RW ドライブ
この他に必要な物が 3 つ。MBP の底面のネジを外す為に必要な#0 の精密ドライバー、HDD に付いているネジを外す為に必要な T6 のトルクスドライバー、HDD から SSD にデータを移す為に必要な USB3.0-SATA 変換ケーブルです。
精密ドライバー #0
トルクスドライバー T6
このベッセルのトルクスドライバーは柄ではなく芯の途中に指のかかりが良くなるようにギザギザが付いていて、弱い力でネジを回したい時など便利です。
USB3.0-SATA 変換ケーブル
データ移行
USB3.0-SATA 変換ケーブルを使って SSD を外付けドライブとして接続して下さい。その状態で MBP をシャットダウンし、command+R を押しながら電源を入れます。 こうする事でディスクユーティリティが起動してきます。
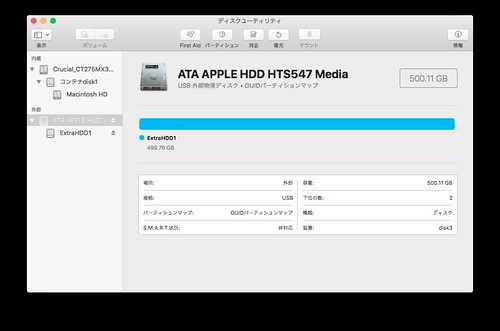
左ペインから移行先の SSD を選択し、上部メニューの復元をクリックすると以下のような画面になります。
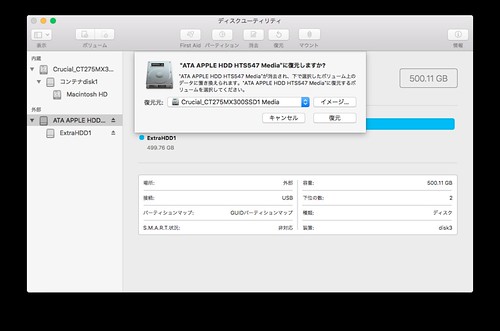
復元もととして、現在使っている HDD を選択して下さい。そして復元をクリックすると、データの移行が始まります。僕は 150GB 程度の使用容量でしたが、USB3.0 接続で 45 分程度で終わりました。
もし復元もとのパーティションが SSD の総容量より大きいとエラーが発生します。その時はディスクユーティリティを使って、復元もとのパーティションサイズと縮小して下さい (これはかなり時間がかかります。途中で MBP がスリープすると進まなくなるので要注意)。
部品交換
では MBP を裏返してネジを外します。外す対象のネジは 10 本あります。ネジの種類は 3 種類。長いネジが 1 種類、短いネジが 2 種類です。短いネジは全ネジが 3 本、段付きネジが 4 本あります。長いネジは 3 本です。これらのネジは比較的硬い素材みたいなので、舐めにくくはなっていますがネジ頭を舐めてしまうと悲惨なので注意して下さい。ネジを回す時の力の入れ具合いは、押す力が 7 割、回す力が 3 割の感覚で。
以下の写真の赤丸が段付きネジ、青丸が全ネジ、黄丸が長いネジです。

これで底面の蓋が取れます。外すと中身は以下のようになっています (以下の写真は既に SSD 交換後)。

右下が HDD/SSD スロットです。右上が DVD スリムドライブです。
HDD/SSD スロット周辺を拡大してみます。

黄丸で囲んだ 4 本のネジを外すと HDD を持ち上げる事が出来ますが、まだ SATA ケーブルが刺さったままなので気を付けて下さい。この 4 本のネジは樹脂のアダプタから完全には抜けません。どれだけ緩めてもアダプタに嵌ったままです。HDD の画面左端に付いている灰色の縦長の部品が SATA ケーブルのコネクタです。これはひっぱれば外れます。
画像を取り忘れましたが HDD 自体に 4 本のネジが付いています。これも外します。この時 T6 のトルクスドライバーが必要になります。
HDD から外した 4 本のネジを SSD に同じように付け、SATA コネクタを装着し、という感じで逆順に SSD を付ければ完了です。
NVRAM のリセット
MBP でハードウェアの交換を行なった後、NVRAM をリセットする必要があります。交換後の初回起動時に以下の手順で NVRAM をリセットして下さい。
2017年11月25日土曜日
心理統計学の基礎 第三章 備忘録
== Sec1
相関関係
$x,y$ の二値が変数の時、$x$ が大きいほど、$y$ も大きい傾向がある場合、正の相関があると言う。
$x$ が大きいほど、$y$ が小さい傾向がある場合、負の相関があると言う。
共分散
$x,y$ の二値が変数の時、$x$ の平均値 $\overline{x}$ と $y$ の平均値 $\overline{y}$ を考える。$x,y$ のそれぞれの値$x_{i}$、$y_{i}$ についてこれらの平均との距離の積の平均値が共分散 $s_{xy}$ になる。つまり
\[
s_{xy} = \frac{1}{N}\sum_{i=1}^{N}(x_{i}-\overline{x}) (y_{i}-\overline{y})
\]
シグマで囲まれた項
\[
(x_{i}-\overline{x}) (y_{i}-\overline{y})
\]
は、xy 平面上で、$x$ の平均値の成す線と $y$ の平均値の成す線から作られる長方形の面積になる。
不偏共分散
不偏分散と同じようにデータ総数 N に対して N-1 で割った共分散を不偏共分散と言う。つまり
\[
s'_{xy} = \frac{1}{N-1}\sum_{i=1}^{N}(x_{i}-\overline{x}) (y_{i}-\overline{y})
\]
完全な正の相関がある 2 変数の共分散は、それぞれの変数の標準偏差の積になる。$xy$ の 2 変数を考えた時、完全な正の相関があるならば $y$ は
\[
y = cx + d
\]
という線形変換が可能である。従って、これを共分散の式に適用すると
\[
s_{xy} = \frac{1}{N}\sum_{i=1}^{N}(x_{i}-\overline{x}) (y_{i}-\overline{y})\\
= \frac{1}{N}\sum_{i=1}^{N}(x_{i}-\overline{x}) [(cx_{i}+d)-(c\overline{x}+d)]\\
= \frac{c}{N}\sum_{i=1}^{N}(x_{i}-\overline{x})^{2}\\
= cs_{x}^{2}\\
= (\frac{s_{y}}{s_{x}}) s_{x}^{2}\\
= s_{x}s_{y}
\]
相関係数
共分散をそれぞれの変数の標準偏差の積で割った値。つまり
\[
r = \frac{s_{xy}}{s_{x}s_{y}}
\]
相関係数の取り得る値は $-1 \leq s_{xy} \leq 1$ になる。
== Sec2
統計的事象は一般的に同じ $x$ の値に対して $y$ は様々な値を取る。例えば、中学生の学習時間 $x$ と試験点数 $y$ の統計の場合、$x$ に対して $y$ は一意に定まらない (同じ学習時間でも試験点数が異なる生徒が存在する)。
条件付き平均
こういった時、1 つの $x$ に対する様々な $y$ の平均を考える。これを $y$ の条件付き平均、と言う。中学生の例で言えば、学習時間が同じ生徒達の平均点数。
回帰直線
$y$ の条件付き平均の予測値 $\hat{y}$ を
\[
\hat{y}=a+bx
\]
とした時の直線の事。
回帰係数
回帰直線の式に於ける変数 $x$ の傾き $b$ の事。
最小二乗法
回帰直線を導く方法の一つ。回帰直線の式に実際観測データ $x_{i}$ を代入して得られる $\hat{y}_{i}$ と、実際の観測データ $y_{i}$ の差の二乗を最小化する $a$、$b$ を求める。つまり
\[
Q = \sum_{i=1}^{N}(y_{i}-\hat{y}_i)^{2}\\
= \sum_{i=1}^{N}[(y_{i}-(a+bx_{i})]^{2}
\]
残差
従属変数の実際の値と予測値ののずれの事。予測の誤差とも言う。残差を $e$ とすると
\[
e = y - \hat{y}
\]
また、残差の平均は
\[
\overline{e} = \overline{y} - \overline{\hat{y}} = 0
\]
となる。
変数の直交
互いに相関が無い ($r=0$) な変数同士は「直交している」と表現する。
残差は独立変数 $x$ との相関が 0 になる (後の章で説明するらしい)。
残差の定義式を変形すると
\[
y = \hat{y} + e
\]
が得られる。$\hat{y}$は独立変数 $x$ の線形変換であるから、$x$ との相関は 1 (または-1) になる。一方残差 $e$ は $x$ とは無相関なので、上記式は $y$ を独立変数と、独立変数とは無関係な値に分解した事になる。
つまり従属変数 $y$ は、独立変数 $x$ だけでは説明できない要素が関連しているという事になる。中学生の例にすると、試験点数は学習時間だけでは説明できない要素があるという事になる (例えば学習の方法の差など)。
残差の分散
予測の誤差分散とも呼ばれ、以下の式で表わされる。
\[
s_{e}^{2} = s_{y}^{2}(1-r^{2})
\]
この平方根
\[
s_{e} = s_{y}\sqrt{1-r^{2}}
\]
は予測の標準誤差と呼ばれる。この予測の標準誤差の大小で予測の精度を評価する事ができる。
対称性
相関係数と回帰係数は共に変数間の関係を表わす指標だが、相関係数はそれぞれの変数に関して対称性がある。つまり $x$ と $y$ の相関係数と、$y$ と $x$ の相関係数は同じになる。しかし回帰係数は非対称になる。$y$ の $x$ への回帰直線と、$x$ の $y$ への回帰直線の傾きは同じにならない。
選抜効果
ある変数の値 (例えば $y$) に基づいてデータの選抜を行なうと、それによって相関係数の値は一般に低下する。この事を選抜効果と呼ぶ。他方、選抜を行なっても回帰係数は殆ど変化しない。
== Sec6
妥当性
測定の妥当性とは、測定値が測定すべきものを正しく反映している程度の事。つまり測定の質。
妥当性の検証
測定が妥当だと仮定して、その場合どのような結果が満たされるか、をリストアップし実際に満たされているか確かめる。
信頼性
測定値の一貫性。同じ測定を繰り返した時、N 回目と N+1 回目で測定値が一貫しているかどうか。
心理統計学の基礎 第二章 備忘録
分布の特徴をあらわす記述的指標
最大値、最小値、平均値 (mean、算術平均) など
調整平均
極端な値の影響を排除する為に最大値、最小値を排除した平均
中央値 (median)
出現する値をソートした時の順位が真ん中になる値
代表値としての適切さ
分布に含まれるそれぞれの値との近さ
データ総数 N
i 番目の実測値 $x_{i}$
1 番目の実測値 $x_{1}$
2 番目の実測値 $x_{2}$
最適な代表値の候補 t
代表値 t とそれぞれ実測値の距離は $|x_{i} - t|$
これの総和を取る
\[
T_{1}=\sum_{i=1}^{N}|x_{i}-t|
\]
$T_{1} $を最小化する値 t が、分布に含まれるそれぞれの値に最も近い。このような基準 $T_{1}$ を最小化する値が中央値。
しかしこの「距離」だと、値の密度が高いあたりの数値影響力が高く、分布の両端にある疎な値の影響力が弱い。
分布の両端 (つまり距離が遠い) 値の影響力を大きくする為に、別の基準 $T_{2}$ を
\[
T_{2}=\sum_{i=1}^{N}(x_{i}-t)^{2}
\]
とすると。代表値 t と各値の二乗を取っているので、距離が遠い=差が大きいものの影響力がより強くなる。このような基準 $T_{2}$ を最小化する値が平均値。
外れ値に対する抵抗性
平均値は中央値に比べて分布の両端の外れた値の影響を強く受ける為、極端な最大値や最小値にひっぱられて平均値は大きく変動する。
一方中央値はこういう極値の影響を受けない。
合成変数
複数の変数に重みを付けた和や差。
変数 x,y、重み c,d の時、合成変数 v は
\[
v = cx + dy
\]
v の平均は
\[
\overline{v} = \frac{1}{N}\sum_{i=1}^{N}v_{i}\\
= \frac{1}{N}\sum_{i=1}^{N}(cx_{i} + dy_{i})\\
= \frac{1}{N}\sum_{i=1}^{N}cx_{i} + \frac{1}{N}\sum_{i=1}^{N}dy_{i}
\]
となる。つまり合成変数の平均は、各変数の平均の和に等しい。
散布度
分布の広がりの程度を表す。
平均偏差
中央値によって最小化される指標$T_{1}$をデータ総数で割った値。つまり
\[
MD = \frac{1}{N}\sum_{i=1}^{N}|x_{i} - Med|
\]
で表わされる。これは各値が中央値から平均してどれくらい離れているかを表わしている。
中央値の代わりに平均値を入れる事もある。
分散
平均値によって最小化される指標$T_{2}$をデータ総数で割った値。つまり
\[
s^{2} = \frac{1}{N}\sum_{i=1}^{N}(x_{i} - \overline{x})^{2}
\]
標準偏差
分散の平方根を取ったもの。つまり
\[
s = \sqrt{\frac{1}{N}\sum_{i=1}^{N}(x_{i} - \overline{x})^{2}}
\]
平均偏差よりも、分散や標準偏差の方が統計的推測では頻繁に使われる。
不偏分散
$T_{2}$をデータ総数ではなく、データ総数-1 で割った値。つまり
\[
s^{2} = \frac{1}{N-1}\sum_{i=1}^{N}(x_{i} - \overline{x})^{2}
\]
線形変換
元の変数 x に対して
\[
x' = cx + d
\]
として新しい変数 x'を得る手続き。
線形変換した x'からそれぞれの指標値を計算すると以下が導出できる。
\[
MD_{x'} = |c| \times MD_{x}\\
s_{x'} = |c| \times s_{x}\\
s^{2}_{x'} = c^{2} \times s_{x}^{2}
\]
上記の用に線形変換後の平均や標準偏差は完全に予測可能なので、変換後の変数が特定の平均と標準偏差を持つように変換する事が可能。
例えば学校で使われる偏差値は、平均 50、標準偏差 10 になるように点数を線形変換したもの。
z 得点
平均を 0、標準偏差を 1 とする線形変換
2017年11月24日金曜日
心理統計学の基礎 第一章 備忘録
== Sec1
リサーチ・クエスチョン
研究上の問い
仮説
問いに対する暫定的な説明
統計的なデータ解析は、
仮説生成
仮説検証
の過程で利用される。
仮説から具体的な予測を論理的に導出し実験やデータ解析で、この予測を支持あるいは棄却する。
あくまで「支持」であって証明ではない。相関と因果は別。
「仮説が正しければ、予測通りの結果が得られる」と前提するならば「予測通りの結果が得られなければ、仮説は正しくない」は対偶なので真であるからデータによって仮説を反証する事は可能。
実際には「仮説が正しければ、予測通りの結果が得られる」という条件を満たせない事が多い (測定が不完全など)。
母集団
サンプル (標本)
標本はランダムに選ばれる事が望ましい
完全な無作為抽出は現実的には困難
== Sec2
度数分布
相関関係
散布図
相関図とも呼ばれる
== Sec3
記述的指標/ 記述統計量/ 要約統計量
分布、広がり、重なりなど
統計的推測
母集団から無作為抽出を過程して確率論的に推測する
2017年11月20日月曜日
D&D 5 版 Sage Advise 抄訳 201710
Q1: バードが読める呪文の巻物はどれですか。バードの呪文リストにあるものだけ? それともマジカル・シークレットの特徴で追加した呪文も読める?
A1: マジカル・シークレットで追加した呪文はバード呪文になるので、これらの呪文の巻物も読めます。
Q2: バトル・マスターが機会攻撃を食って、それが外れた時、このバトル・マスターはリポストの戦技で反撃出来ますか。
A2: はい、バトル・マスターのリアクションがまだ残っているならば。
Q3: モンクがエンプティ・ボディの能力で透明化した時、そのモンクが攻撃してもまだ透明化は続きますか。
A3: はい。
Q4: パラディンがラスフル・スマイト (wrathful smite) のようなスマイト系の呪文を使った上で、その攻撃が命中した時にディヴァイン・スマイトも乗せられますか?
A4: はい。
Q5: エレメンタル・アフィニティの特徴は呪文の 1 つのダメージ・ロールにのみ加算可能ですか? 例えばスコーチング・レイで 3 本のレイを撃った時、それぞれに【魅力】修正を足せる?
A5: いいえ。いずれか 1 つです。
Q6: アイズ・オブ・ザ・ルーン・キーパーのインヴォケーションは魔法のルーンにも機能しますか。
A6: アイズ・オブ・ザ・ルーン・キーパーは、記述されたものであれば何でも読めるようにします。それがルーンであっても言語的意味であっても、です。
Q7: 変成術系統のシェイプチェンジャーの特徴を持ったウィザードは、ポリモーフの呪文をスロット消費なしに使えますが、そもそそもポリモーフの呪文を準備する必要はありますか。
A7: はい
Q8: 《ダンジョン・デルヴァー》の特技には、罠の捜索を旅のあいだであっても通常の速度で行なえるとありますが、そもそも罠捜索の速度のルールって存在しますか。
A8: しません。この文は無視して下さい。
Q9: 《センチネル》の特技を持っているキャラクタは、ファンシィ・フットワークの特徴や《モバイル》の特技を持った相手に機会攻撃出来ますか。
A9: いいえ。《センチネル》の 2 つめの利益は、離脱アクションを試みた相手にも機会攻撃が可能、というものです。ファンシィ・フットワークにしろ《モバイル》にしろ、これらは離脱アクションではありません。
Q10: キャラクタが 20 レベルになった後はどうなりますか。20 レベルがキャラクタの最大レベル?
A10: ダンジョン・マスターズ・ガイドの「エピック・ブーン」のセクションを読みましょう。
Q11: もし私が貴方に組みつきをしたとします。更にその状態で私は自発的に伏せ状態になったら、貴方も一緒に伏せになる?
A11: いいえ。伏せた状態の貴方が、立っている私に組みついている状態になるだけです。
Q12: チル・タッチの呪文は再生を止めますか。
A12: はい。チル・タッチはその効果時間中、あらゆるヒット・ポイント回復を阻害します。
Q13: ジャンプの呪文によって、跳躍の飛距離が通常移動速度 (walk speed) よりも大きくなった時、どう処理すれば良いですか。
A13: 跳躍による移動も通常移動速度による制限を受けます。もし通常移動速度を超えて跳躍するならば早足アクションを取る必要があります。
Q14: メイジ・アーマーの呪文の名前に混乱しています。だってアーマーって言ってるのに鎧と見做さないんだもの。
A14: いくつかの呪文やクラスの特徴の名称は、比喩的なので字義的なものではありません。呪文やクラス特徴の詳細な説明文が実際に発生する事を説明しています。
Q15: どんな物がプレスティディジテーションの為の非魔法の小物と見做されますか。
A15: プスティディジテーションは、小さく安価な物を作り出す事が出来ます。その物がどんなものかは呪文を使った本人と DM が決めて下さい。
Q16: ストーム・オブ・ヴェンジェンス呪文の効果は累積しますか。あるいは、毎ターン効果が変わる? [訳注: Or do the effects change each turn? の意図が分からない]
A16: それぞれの新しい効果が前のラウンドの効果を上書きします。[訳注: この解答もよくわからないが、each new effect と言っているので呪文の効果自体は累積するっぽい]
Q17: グールとギャストの噛み付き攻撃には習熟ボーナスが加算されていないようですが、これはミス? それともわざと?
A17: 意図的です。
Q18: エアー/ ファイア/ ウォーター・エレメンタルは、5 フィートよりも狭い空間でペナルティなく戦えますか。
A18: エアー/ ファイア/ ウォーター・エレメンタルは、移動の時に無理矢理入り込むペナルティを無視出来ます。
Q19: アース・エレメンタルが相手に組み付いた状態で、そのまま地下へ引きずり込んだら相手は死にますか?
A19: いいえ。アース・エレメンタルのアース・グライドの能力は自分自身にだけ機能します。つまりこの場合、アース・エレメンタルだけが地下へ移動し、組み付かれた側は地上に残ります。
Q20: リッチのディスラプト・ライフの能力はアニメイテッド・オブジェクトやコンストラクト相手にも機能しますか。
A20: はい。相手がアンデッドでなければ機能します。
Q21: ヴァンパイアは同時にチャーム可能なクリーチャーの数に上限はありますか。
A21: いいえ。一回のチャームアクションで魅了出来るクリーチャーは 1 体ですが、それを何回も実行すれば同時にチャーム出来ます。
Q22: バードがインストルメント・オブ・ザ・バーズのマジックアイテムに同調していて、かつそれを手に保持した状態で、チャーム・パーソンを使ったら対象のセーヴには不利が付きますか?
A22: いいえ。インストルメント・オブ・ザ・バーズは、それを呪文発動時の焦点具として利用した時のみ、相手を魅了状態にする呪文のセーヴに不利を付けられます。しかしチャーム・パーソンは物質要素が無い呪文なので、インストルメントは効果を発揮しません。[訳注: 通常、呪文発動時の焦点具は物質要素の代わりに使うので、物資要素が無い呪文の場合焦点具は使われない]
Q23: アサシネイトの能力を持ったローグがヴォーパル・ソードを装備して、不意打ちで攻撃したら相手は即死?
A23: いいえ。ヴォーパル・ソードで相手を即死させるには、20 面体を振って出目 20 を出す必要があります。アサシン・アーキタイプのローグによる不意打ちの攻撃は、自動クリティカルであって出目 20 ではありません。
2017年11月19日日曜日
【今日の読書】コンピューターで「脳」がつくれるか
著者: 五木田 和也
出版: 技術評論社
ISBN: 978-4-7741-8410-4
現在の人工知能にまつわる主要なキーワードについて、それぞれ噛み砕いて説明した本です。数式や難解な用語は避けているのですが、何故か四章の脳科学の部分だけやたらと専門用語が連発されて、他の章との不均衡を感じます。多分そのあたりが筆者の専門分野なのでしょう。四章だけ興が乗ってキーボードが滑ったのかもしれません。
人工知能の大雑把な歴史、特化型人工知能と汎用人工知能の違いなど抑えるべき点をさらっと 200 ページに見たない本で説明しているので、概観を捉えたい人に向いた本です。
2017年11月18日土曜日
Princes of the Apocalypse 7 [72]
アンドリュー、 Cleric (War) 1/Warlock (Blade Pact) 7, Half-Elf, CG, ほえほえさん
シマズ, Figher (Champion) 8, Half-Orc, LN, からくりさん
スパイア, Sorcerer (Storm) 3 / Paladin (Crown) 5, Tabaxi, LG, つかださん
ツリートップ, Bard (Lore) 8, Tabaxi, CG, さるしんごさん
ミック, Monk (Sunsoul) 8, Tabaxi, CG, いっちゃん
メルゲン, Fighter (Battle Master) 8, Human, TN, 六平さん
ユーウェイン, Wizard (Bladesinger) 8, High Elf, CG, 死せる詩人
前半はヤーター街で開かれているバザールで各人個人的パワーアップという名のマジックアイテム探し。
アンドリュー: ガントレット・オブ・オーガパワー
シマズ: ウィングド・ブーツ
スパイア: センチネル・シールド
ツリートップ: フォークルカン・バンドーラ
ミック: クローク・オブ・レジスタンス
メルゲン: ゴーグル・オブ・ナイト
ユーウェイン: フレイム・タン
をそれぞれ 1 万から 2 万ゴールドほどで購入。さらに余った金やらアイテムで、シマズ用にグレート・ソード +2 を入手。
その後の街の有力者という名のヤクザ者のどちらに付くかという決断を迫られ、シナリオに必要そうなアイテムを持っている元川賊の女傑につき、相手の組にかちこみ。したと思ったら相手がサハギンで驚きつつ、サハギン・バロンっぽいボス、ヒドラ、ウォーター・エレメンタル、サハギン・クレリック 6 体を撃破。デヴァーステーティング・オーブなるテロリズム誘発アイテムを鹵獲。
戦闘。#DnD pic.twitter.com/9GqTSZVo2t
— 死せる詩人 (@siseru) 2017年11月18日
ヒドラ登場。猫が食われる。#DnD pic.twitter.com/1r4siaY3ss
— 死せる詩人 (@siseru) 2017年11月18日
バザールも終わったので、ユーウェインが 9 レベルで覚えたテレポーテション・サークルでレッドラーチへ帰還。依頼主にデヴァーステーティング・オーブ 6 個を渡す。
以前見付けて、その時点では身の丈に合わないという事で回避したリバーガード・キープ地下のダンジョンへ。ウォーター・カルトを殲滅すべし。
道中ヒル・ジャイアント 6 体に遭遇するが、不意打ち出来たのとユーウェインが無茶苦茶ジャイアントの生態に詳しいのがあって比較的余裕で撃破。
リバーガード・キープ地下ではいきなりドラゴン・タートル (モンスター・マニュアル通りなら CR17!!) に出会うがスパイアが冷静に交渉し、ウォーター・カルトを快く思っていなかった亀さんと友好的に話し合いを終える。
ガメラ……じゃなかった、ドラゴンタートルが川底から登場。#DnD pic.twitter.com/PAkISfxptO
— 死せる詩人 (@siseru) 2017年11月18日
その後サハギン・プリースト 3 体、中堅カルト員 4 人、4 本腕のストーン・ゴレームを倒した所で時間切れ。
ストーンゴーレム #DnD pic.twitter.com/SZAEgSp6Js
— 死せる詩人 (@siseru) 2017年11月18日
ここでセーブして次回は続きから。
【今日の読書】キーポイント 線形代数
著者: 薩摩 順吉、四ツ谷 晶二
出版: 岩波書店
ISBN: 978-4-00-007862-7
機械学習やディープラーニング関連のプログラミングをすると線形代数(行列計算)の知識が必要になってくるので「キーポイント 確率・統計」と同じシリーズの線形代数の本を読んでみました。
これは名著です。特に前半が非常に分かりやすく、2x2や3x3の行列を意識的に例に取っているのもあって概念的な部分もかなり頭に入り易いです。
行列のおさらいをしたいという目的にはかなり向いた本と言えると思います。
2017年11月15日水曜日
【今日の読書】キーポイント 確率・統計
著者: 和達 三樹、十河 清
出版: 岩波書店
ISBN: 978-4-00-007866-5
「はじめてのパターン認識」を読み始めたものの、統計関連の用語がさっぱりだったのでまず統計学の初歩を抑えておかねばと思って探した本。150 ページ程度でかなりうすいけれど初歩はさらえます。ただ式展開や証明など飛ばしている所もあるので、もしそのあたりを知りたければ別の本に頼る必要があります。
しかし機械学習の勉強の準備として統計学を知りたいならこの程度でも充分かもしれません。
2017年11月12日日曜日
【今日の読書】ゼロから作る Deep Learning
著者: 斎藤 康毅
出版: オライリー・ジャパン
ISBN: 978-4-87311-758-4
非常に良い本。とりあえず写経しつつ読んだが、おりに振れて読み返す事になりそう。
目次
まえがき
1 章 Python 入門
2 章 パーセプトロン
3 章 ニューラルネットワーク
4 章 ニューラルネットワークの学習
5 章 誤差逆伝播法
6 章 学習に関するテクニック
7 章 畳み込みニューラルネットワーク
8 章 ディープラーニング
2017年11月7日火曜日
【今日の読書】データサイエンティスト養成読本 機会学習入門編
著者: 比戸将平、馬場雪乃、里洋平、戸嶋龍哉、得居誠也、福島真太朗、加藤公一、関喜史、阿部厳、熊崎宏樹
出版: 技術評論社
ISBN: 978-4-7741-7631-4
第 1 部
しくみと概要を学ぼう!
特集 1
機械学習を使いたい人のための入門講座…… 比戸将平
第 1 章:機械学習の概要
第 2 章:機械学習の歴史と今後の応用例
第 3 章:データサイエンティストのための機械学習
第 4 章: Q&A とまとめ
特集 2
機械学習の基礎知識…… 馬場雪乃
第 1 章:機械学習の問題設定
第 2 章:教師あり学習
第 3 章: 教師なし学習
第 4 章:応用
特集 3
ビジネスに導入する機械学習…… 里 洋平・戸嶋龍哉
第 1 章:ビジネスデータのクラスタリング
第 2 章:予測モデルの構築
特集 4
深層学習最前線…… 得居誠也
第 1 章:準備
第 2 章:多層パーセプトロンの書き方
第 3 章:ニューラルネットの学習方法
第 4 章:画像認識のためのアーキテクチャ
第 2 部
手を動かして学ぼう!
特集 1
機械学習ソフトウェアの概観…… 福島真太朗
第 1 章:開発が進む機械学習のソフトウェア
第 2 章:機械学習のソフトウェアを用いた実行例
第 3 章:機械学習ソフトウェア選択の指針
特集 2
Python による機械学習入門…… 加藤公一
第 1 章:イントロダクション
第 2 章: Numpy , Scipy , matplotlib の基礎
第 3 章: scikit-learn 入門
特集 3
推薦システム入門…… 関 喜史
第 1 章:推薦システムのキホン
第 2 章:推薦システムを作る
第 3 章:推薦システムの高度化
第 4 章:良い推薦システムを作るために
特集 4
Python で画像認識にチャレンジ…… 阿部 厳
第 1 章:画像認識とは?
第 2 章:準備
第 3 章:シンプルな画像認識を実装
第 4 章:猫顔検出に挑戦
特集 5
Jubatus による異常検知…… 熊崎宏樹
第 1 章:はじめに
第 2 章:アーキテクチャ
第 3 章:テストデータからの異常検知
第 4 章:サーバログからの異常検知
2017年11月4日土曜日
Dead in Thay [71]
ミック, Barbarian (Path of Berserker) 9, Human, 満月
スカーレット, Paladin (Oath of the Ancients) 9, Tiefling, からくり
三代目, Cleric (Life Domain) 1/Bard (College of Lore) 8, Human, いっちゃん
マリーマリー, Rogue (Mastermind) 3/Bard (College of Lore) 6, Tiefling, 羽生
ペライオス, Sorcerer (Wild Magic) 9, Tiefling, 死せる詩人
シナリオは Tales from the Yawing Portal に掲載されている「Dead in Thay」です。9 レベルから 11 レベル対応のダンジョンシナリオです。サーイの地下にあるダンジョンに、リッチの経箱が沢山格納された部屋があるので、そこを発見し経箱を壊しまくろう! という趣旨。
エリア毎にモンスタの傾向が多きく違い、様々なモンスタと戦える趣向になっています。今回は 3 エリアほど回って時間切れ。
2017年11月2日木曜日
【今日の読書】改訂 2 版 データサイエンティスト養成読本
著者: 佐藤洋行、原田博植、里洋平、和田計也、早川敦士、倉橋一成、下田倫大、大成浩子、奥野晃裕、中川帝人、長岡裕己、中原誠
出版: 技術評論社
ISBN: 978-4-7741-8360-2
目次
巻頭企画
データサイエンティストの仕事術
第 1 章:データサイエンティストに必要なスキル
第 2 章:データサイエンスのプロセス
第 3 章:「ビッグデータインフラ」入門
特集 1
データ分析実践入門
第 1 章: R で統計解析をはじめよう
第 2 章: RStudio でらくらくデータ分析
第 3 章: Python による機械学習
第 4 章:データマイニングに必要な 11 のアルゴリズム
特集 2
マーケティング分析本格入門
第 1 章: R によるマーケティング分析
第 2 章: mixi における大規模データマイニング事例
第 3 章:ソーシャルメディアネットワーク分析
特別記事
Fluentd 入門
特別企画
データ分析のためにこれだけは覚えておきたい基礎知識
第 1 章: SQL 入門
第 2 章: Web スクレイピング入門
第 3 章: Tableau 実践入門
2017年11月1日水曜日
【今日の読書】データサイエンティスト養成読本 登竜門編
著者: 高橋 淳一、野村 嗣、西村 隆宏、水上 ひろき、林田 賢二、森 清貴、越水 直人、露崎 博之、早川 敦士、牧 允皓、黒柳 敬一
出版: 技術評論社
ISBN: 978-4-7741-8877-5
書名通りの本です。「戦略的データサイエンス入門」より先にこちらを読んだ方が良いかも。
データサイエンティストという職種は、技術的知識に限って言ってもかなり広範な知識が求められるので、それらをそれぞれ概説している本です。読んだ以後データサイエンスに対する見通しが良くなって、自分の学習方向性が見えてくると思います。
目次
なぜデータ分析が必要なのか -データサイエンティストへの道標
プロセス別にみるツールの選択基準 -データ分析環境構築ガイド
世界中の環境に接続! -はじめてのシェル
データ操作の第一歩 -データベース入門の入門
美しい分析をはじめよう -RStudio/Jupyter 最速攻略
データ分析オーバービュー -データ前処理の基礎知識
集計、グラフ作成、回帰分析 -くらべて学ぶ R/Excel データ分析の基本
Python のコードを読んで学ぶ -クローラで Web 上の情報を収集しよう!
データがつくられる背景を知る -コーディング前に知りたい統計知識
数理モデルと可視化 -さまざまなデータの理解と表現
重点ポイントを速攻習得!